P5JS Tetrahedron

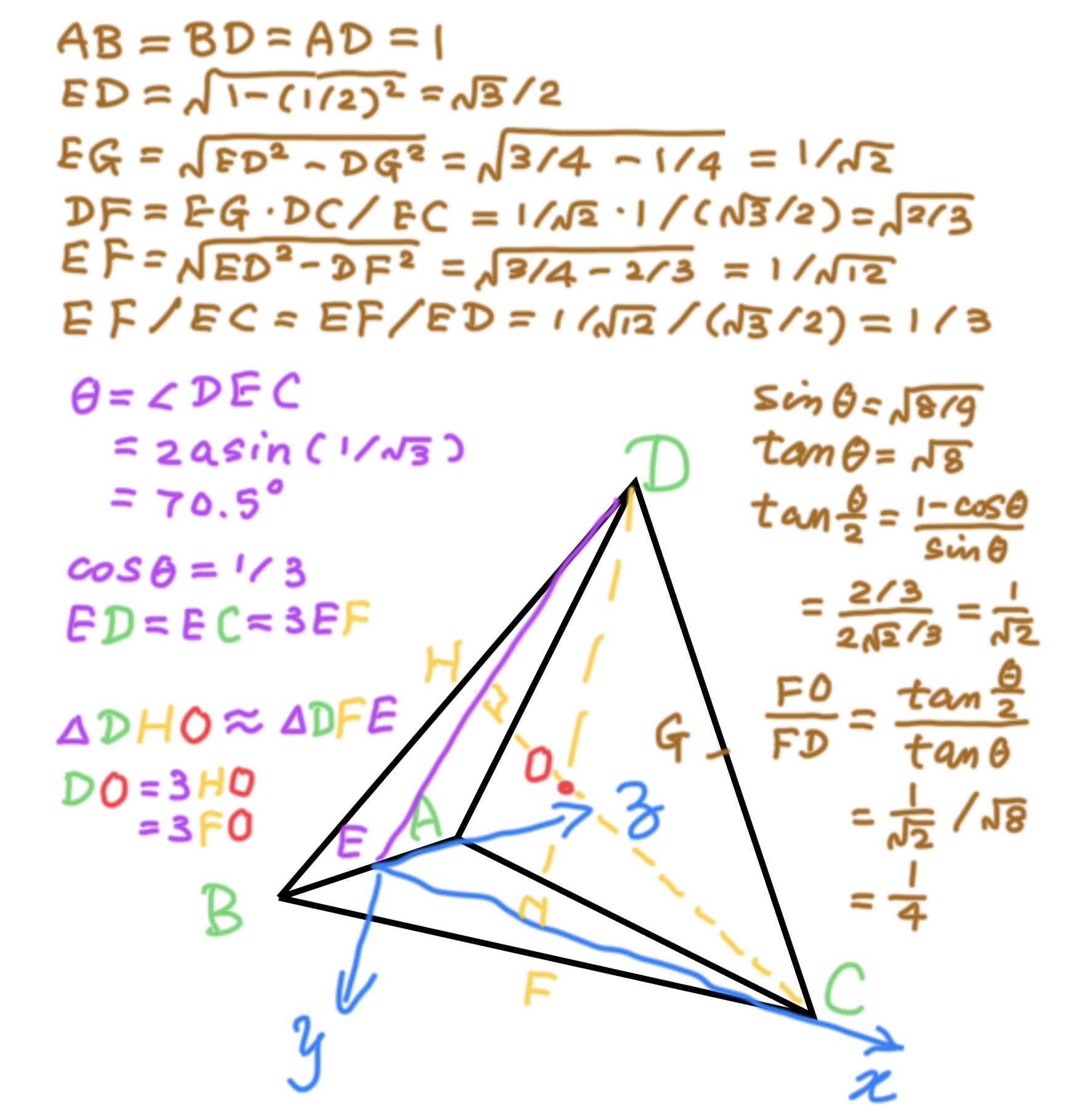
What is interesting is

EC = 3EF
FD = 4FO

cosθ = 1/3
sinθ = √8/3
tanθ = √8
tan(θ/2) = (1-cosθ)/sinθ
         = 1/√2
FO/FD = tan(θ/2)/tanθ = 1/4

This is what it looks like when finished:

Our goal is to let the tetrahedron ABCD spin slowly around its center, which is also the origin of our 3D coordinates space. To make the calculation easier, we start with setup where origin stays at point E, the center of edge AB.

Let side of the tetrahedron AB = u. Then AE = BE = u/2. If we translate origin from the center of tetrahedron to point E, and let DE = CE = v, which is (√3/2)u, we get coordinates of vertices A, B and C as following.

A(0, 0,  u/2)
B(0, 0, -u/2)
C(v, 0,    0)

To figure out the position of vertex D, let us look at isosceles triangle DEC. Let angle DEC be theta. It's easy to see sin(theta/2) = (DC/2)/DE = (u/2)/v = 1/√3. So theta = 2arcsin(1/√3).

D(v*cos(theta), -v*sin(theta), 0)

To translate origin to point E, x goes by -v*cos(theta), y goes by v*cos(theta)*tan(theta/2), z doesn't change. y's formula comes from isosceles triangle DEC.

draw a sphere centered at origin

translate down and left to draw the bottom face

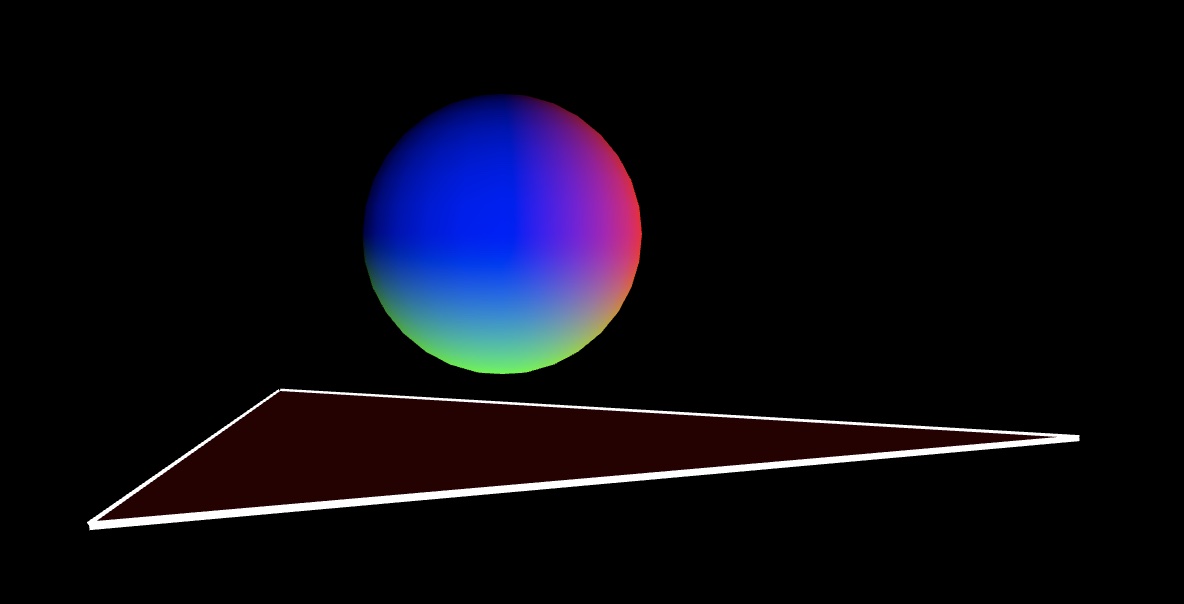
translate down and left and rotate around z-axis to draw the left face

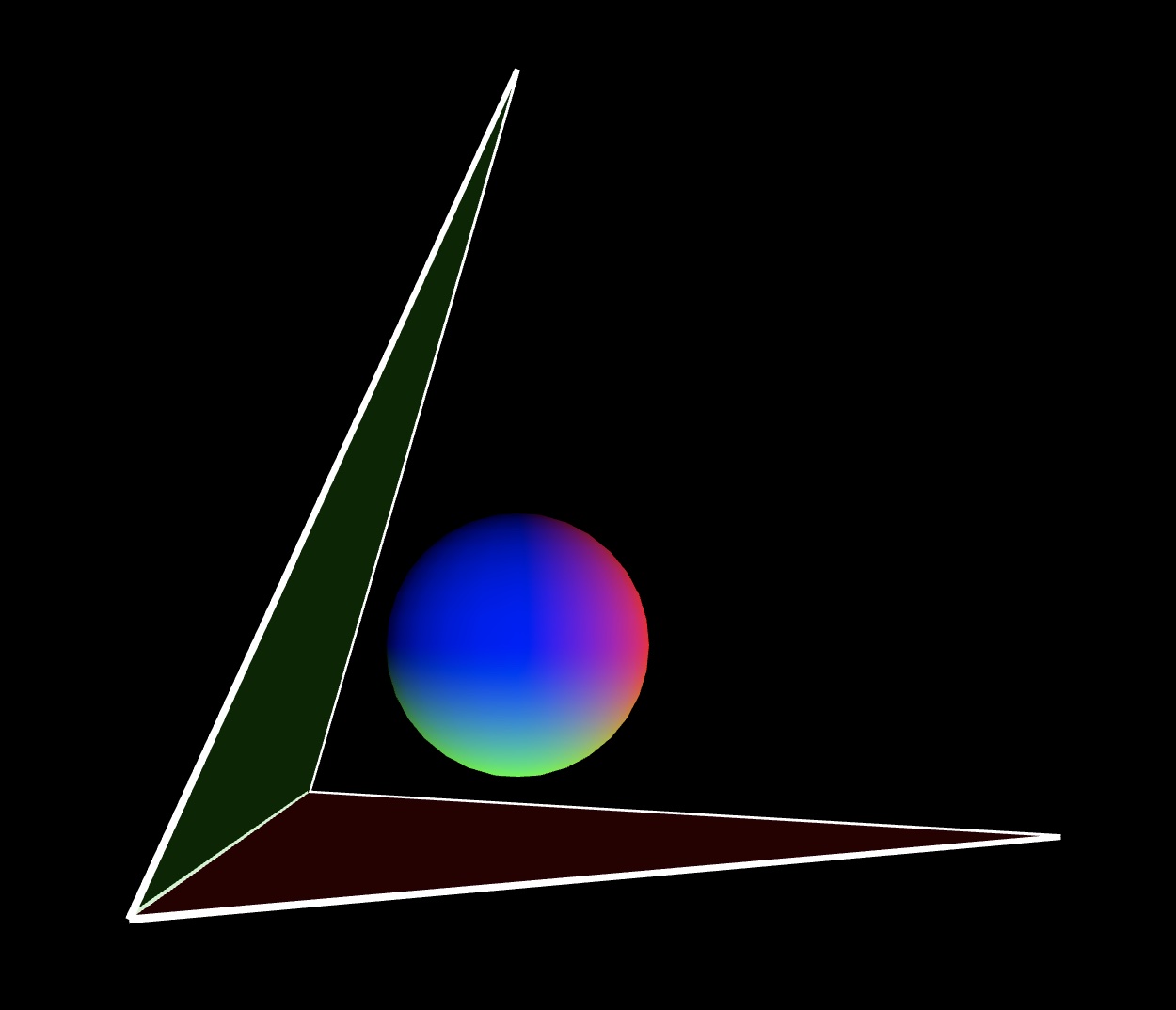
translate down and left draw the face close to our eyes, we don't draw the back face, the 4th one

file tetrahedron.html


    
<!DOCTYPE html>
<html lang="en">
<head>
  <title>正四面体 Tetrahedron</title>
  <meta name="viewport"
        content="width=device-width, 
                 initial-scale=1" />
  <script src=
    "https://cdnjs.cloudflare.com/
     ajax/libs/p5.js/1.5.0/
     p5.min.js">
  </script>
  <style>
    canvas {
      width: 100% !important;
      height: 100% !important;
    }
  </style>
  <meta charset="utf-8" />
</head>
<body>
  <p>
    正四面体 Tetrahedron
  </p>
  <script src=
    "/scripts/tetrahedron.js">
  </script>
</body>
</html>

file tetrahedron.js


let ang = 0;
let u = 500;
let v;
let theta;

function setup() {
  createCanvas(960, 960, WEBGL);
  stroke(255);
  strokeWeight(3);
  v = u * sqrt(3) / 2;
  theta = 2 * asin(1/sqrt(3));
}

function draw() {
  background(0);
  normalMaterial();
  let aX = 0;
  let aY = 0;
  let aZ = u/2;
  let bX = 0;
  let bY = 0;
  let bZ = -u/2;
  let cX = v;
  let cY = 0;
  let cZ = 0;
  let dX = v * cos(theta);
  let dY = -v * sin(theta);
  let dZ = 0;

  rotateY(ang);
  rotateX(ang*0.5);
  rotateZ(ang*0.2);
  strokeWeight(15);
  sphere(70);

  push();
  fill(200, 0, 0, 50);
  stroke(255);
  strokeWeight(10);
  stroke(255);
  strokeWeight(3);
  translate(-v*cos(theta), 
            v*cos(theta)*tan(theta/2), 
            0);
  beginShape();
  vertex(aX, aY, aZ);
  vertex(bX, bY, bZ);
  vertex(cX, cY, cZ);
  endShape(CLOSE);
  pop();

  push();
  fill(0, 200, 0, 50);
  stroke(255);
  strokeWeight(3);
  translate(-v*cos(theta), 
            v*cos(theta)*tan(theta/2), 
            0);
  rotateZ(-theta);
  beginShape();
  vertex(aX, aY, aZ);
  vertex(bX, bY, bZ);
  vertex(cX, cY, cZ);
  endShape(CLOSE);
  pop();

  push();
  fill(0, 0, 200, 50);
  stroke(255);
  strokeWeight(3);
  translate(-v*cos(theta), 
            v*cos(theta)*tan(theta/2), 
            0);
  beginShape();
  vertex(aX, aY, aZ);
  vertex(dX, dY, dZ);
  vertex(cX, cY, cZ);
  endShape(CLOSE);
  pop();

  ang += 0.01;
}

If we keep the origin unchanged, the coordinates of 4 vertices will be

A(-v/3, v/3*tan(θ/2),  u/2)
B(-v/3, v/3*tan(θ/2), -u/2)
C(2v/3, v/3*tan(θ/2),    0)
D(   0,  -v/tan(θ/2),    0)

since tan(θ/2) = 1/√2

A(-v/3, v/(3√2),  u/2)
B(-v/3, v/(3√2), -u/2)
C(2v/3, v/(3√2),    0)
D(   0, -v/(√2),    0)


let ang = 0;
let u = 500;
let v;
let theta;

function setup() {
  createCanvas(960, 960, WEBGL);
  stroke(255);
  strokeWeight(3);
  v = u * sqrt(3) / 2;
  theta = 2 * asin(1/sqrt(3));
}

function draw() {
  background(0);
  normalMaterial();
  let aX = -v/3;
  let aY = v/(3*sqrt(2));
  let aZ = u/2;
  let bX = -v/3;
  let bY = v/(3*sqrt(2));
  let bZ = -u/2;
  let cX = (2/3)*v;
  let cY = v/(3*sqrt(2));
  let cZ = 0;
  let dX = 0;
  let dY = -v/sqrt(2);
  let dZ = 0;

  rotateY(ang);
  rotateX(ang*0.5);
  rotateZ(ang*0.2);
  strokeWeight(15);
  sphere(70);

  push();
  fill(200, 0, 0, 50);
  stroke(255);
  strokeWeight(10);
  stroke(255);
  strokeWeight(3);
  triangleShape(
    [aX, aY, aZ],
    [bX, bY, bZ],
    [cX, cY, cZ]);
  pop();

  push();
  fill(0, 200, 0, 50);
  stroke(255);
  strokeWeight(3);
  triangleShape(
    [aX, aY, aZ],
    [bX, bY, bZ],
    [dX, dY, dZ]);
  pop();

  push();
  fill(0, 0, 200, 50);
  stroke(255);
  strokeWeight(3);
  triangleShape(
    [aX, aY, aZ],
    [dX, dY, dZ],
    [cX, cY, cZ]);
  pop();

  ang += 0.01;
}

function triangleShape(p1,p2,p3) {
  beginShape();
  vertex(p1[0], p1[1], p1[2]);
  vertex(p2[0], p2[1], p2[2]);
  vertex(p3[0], p3[1], p3[2]);
  endShape(CLOSE);
}

further refactored t shorten the code



let ang = 0, u = 500, v;

function setup() {
  createCanvas(960, 960, WEBGL);
  stroke(255);
  strokeWeight(3);
  v = u * sqrt(3) / 2;
}
function draw() {
  background(0);
  normalMaterial();
  let a = [-v/3, v/(3*sqrt(2)), u/2];
  let b = [-v/3, v/(3*sqrt(2)), -u/2];
  let c = [(2/3)*v, v/(3*sqrt(2)),0];
  let d = [0, -v/sqrt(2), 0];

  rotateY(ang);
  rotateX(ang*0.5);
  rotateZ(ang*0.2);
  strokeWeight(15);
  sphere(70);
  stroke(255);
  strokeWeight(3);

  triangleShape(a,b,c,200,0,0);
  triangleShape(a,b,d,0,200,0);
  triangleShape(a,d,c,0,0,200);

  ang += 0.01;
}
function triangleShape(i,j,k,r,g,b){
  push();
  fill(r, g, b, 50);
  beginShape();
  vertex(i[0], i[1], i[2]);
  vertex(j[0], j[1], j[2]);
  vertex(k[0], k[1], k[2]);
  endShape(CLOSE);
  pop();
}

ch 2.2 The Regular Polyhedra p21 of

Tetrahedron

© muzhi 2023