This is what it looks like when finished:

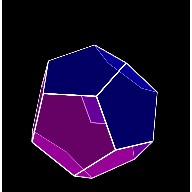
First we want to calculate the angle between any 2 adjacent ⬠ faces, β in the above diagram. There is a generic relation between β and ⍺. In our specific case of dodecahedron ⍺ = 108º. So β = 116.7º.

draw the bottom ⬠ :

the 1st ⬠ adjacent to the bottom ⬠ :

the 2nd ⬠ adjacent to the bottom ⬠ :

the 3rd ⬠ adjacent to the bottom ⬠ :

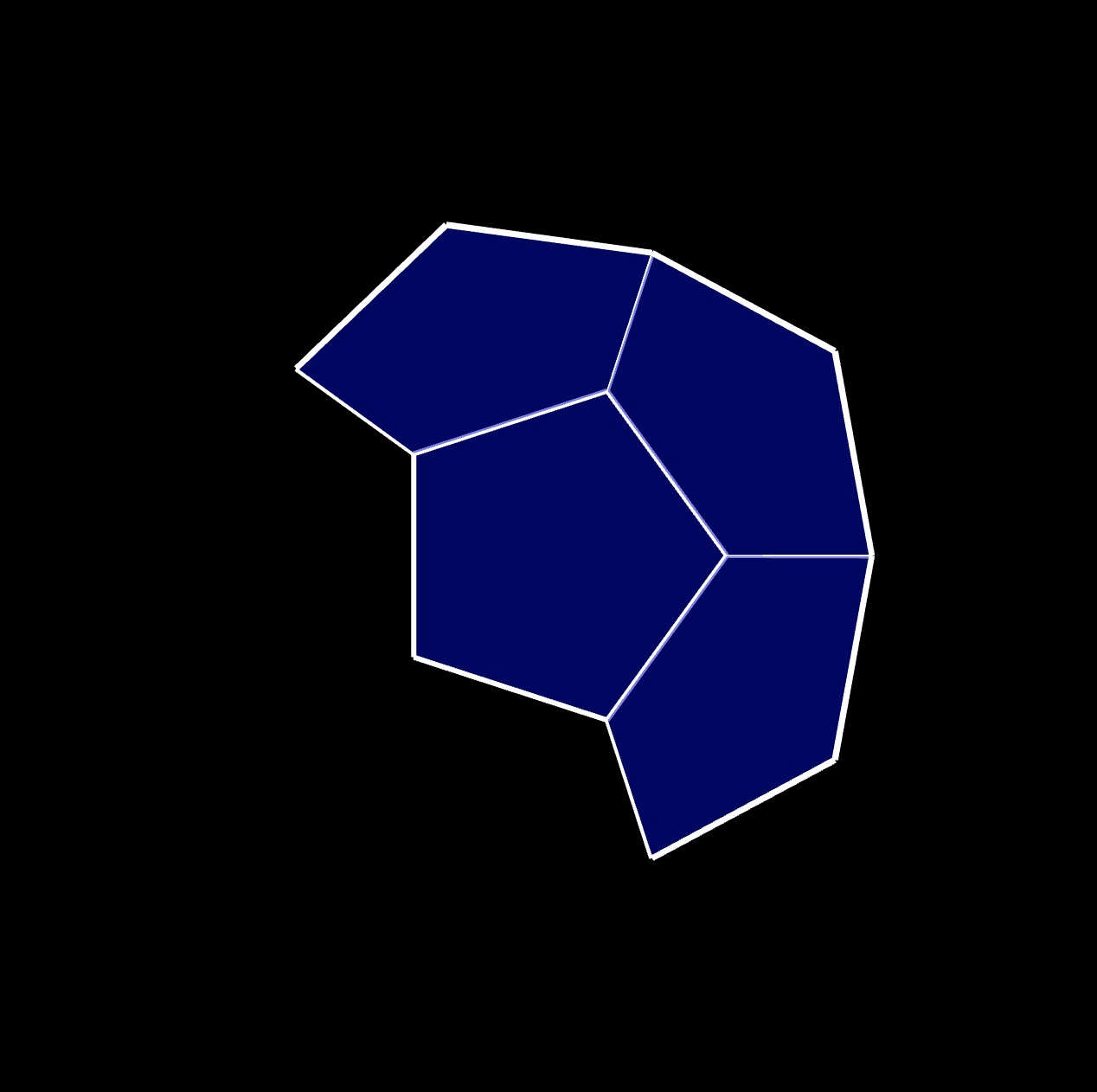
draw the 4th ⬠ adjacent to the bottom ⬠ :

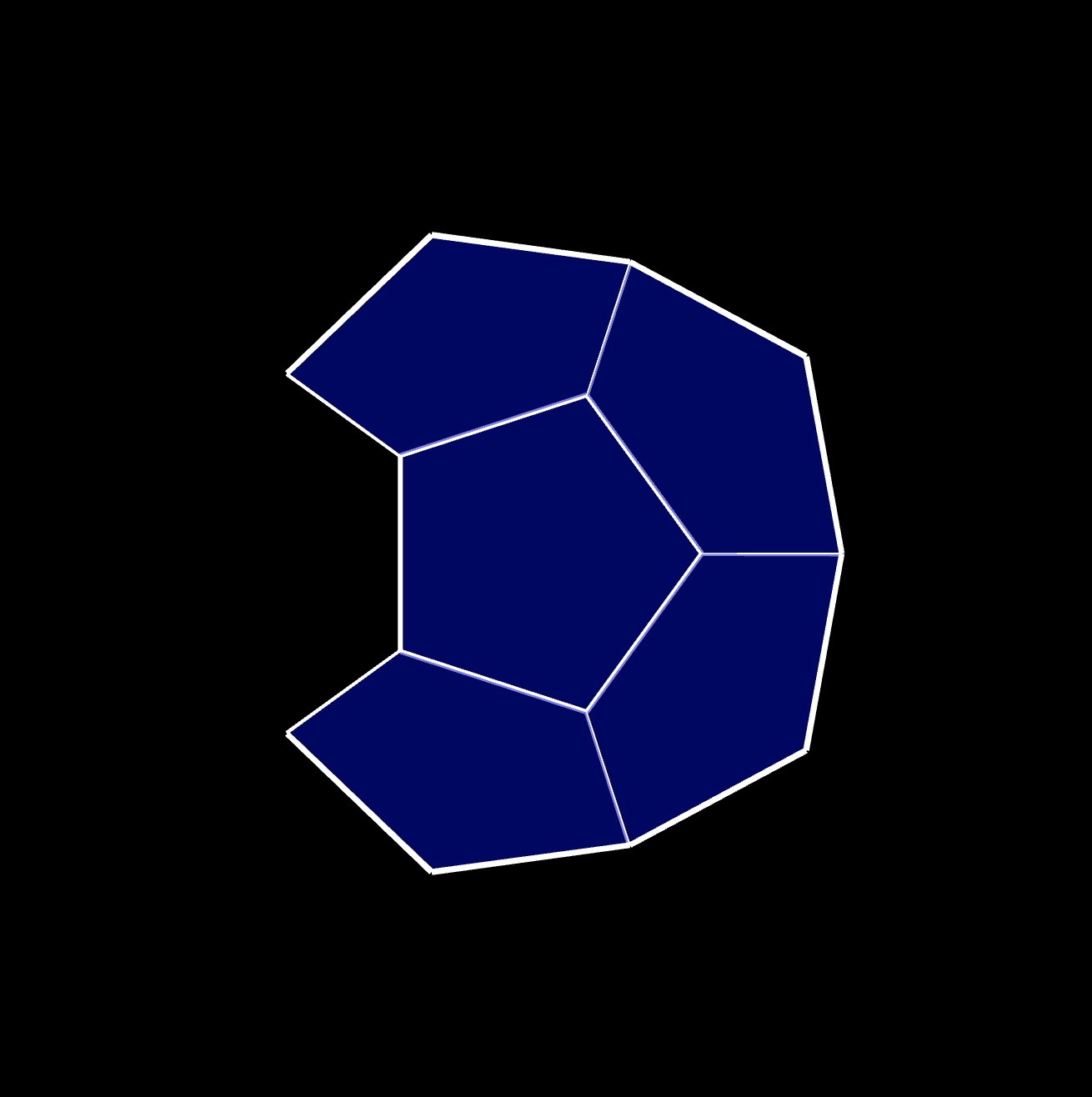
the last ⬠ adjacent to the bottom ⬠ :

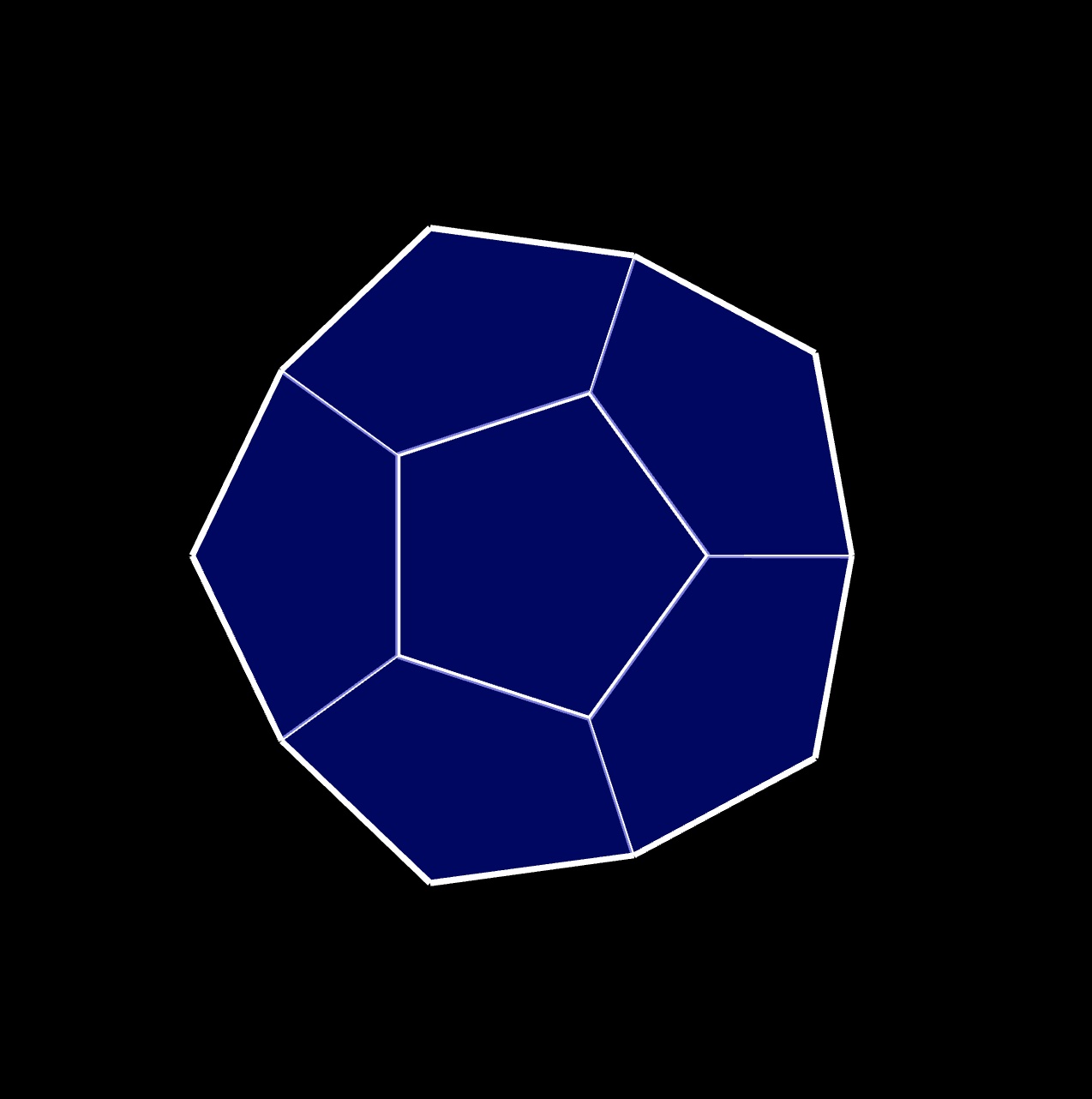
the top ⬠ facing the bottom ⬠ :

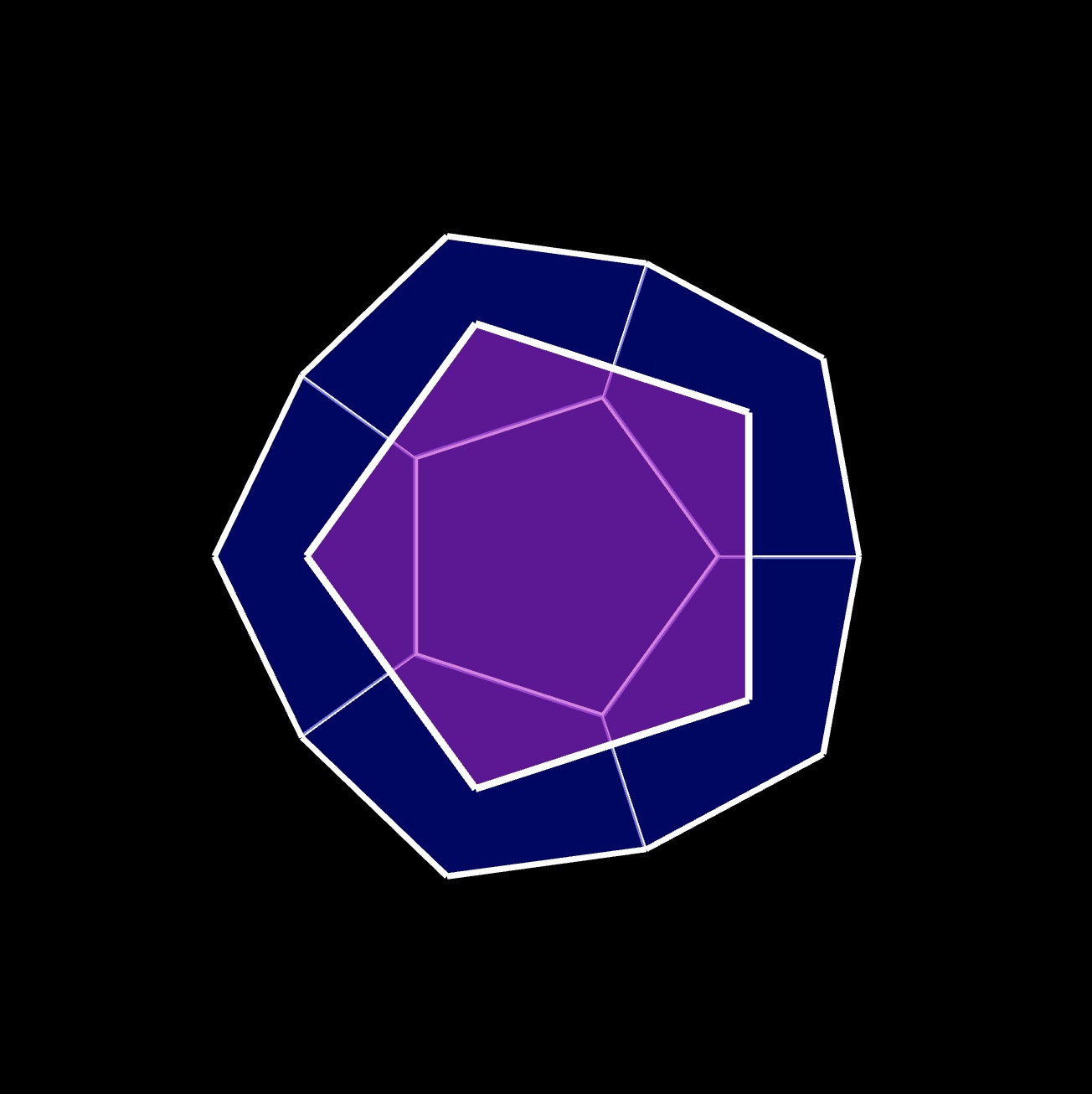
the 1st ⬠ adjacent to the top ⬠ :

the 2nd ⬠ adjacent to the top ⬠ :

the 3rd ⬠ adjacent to the top ⬠ :

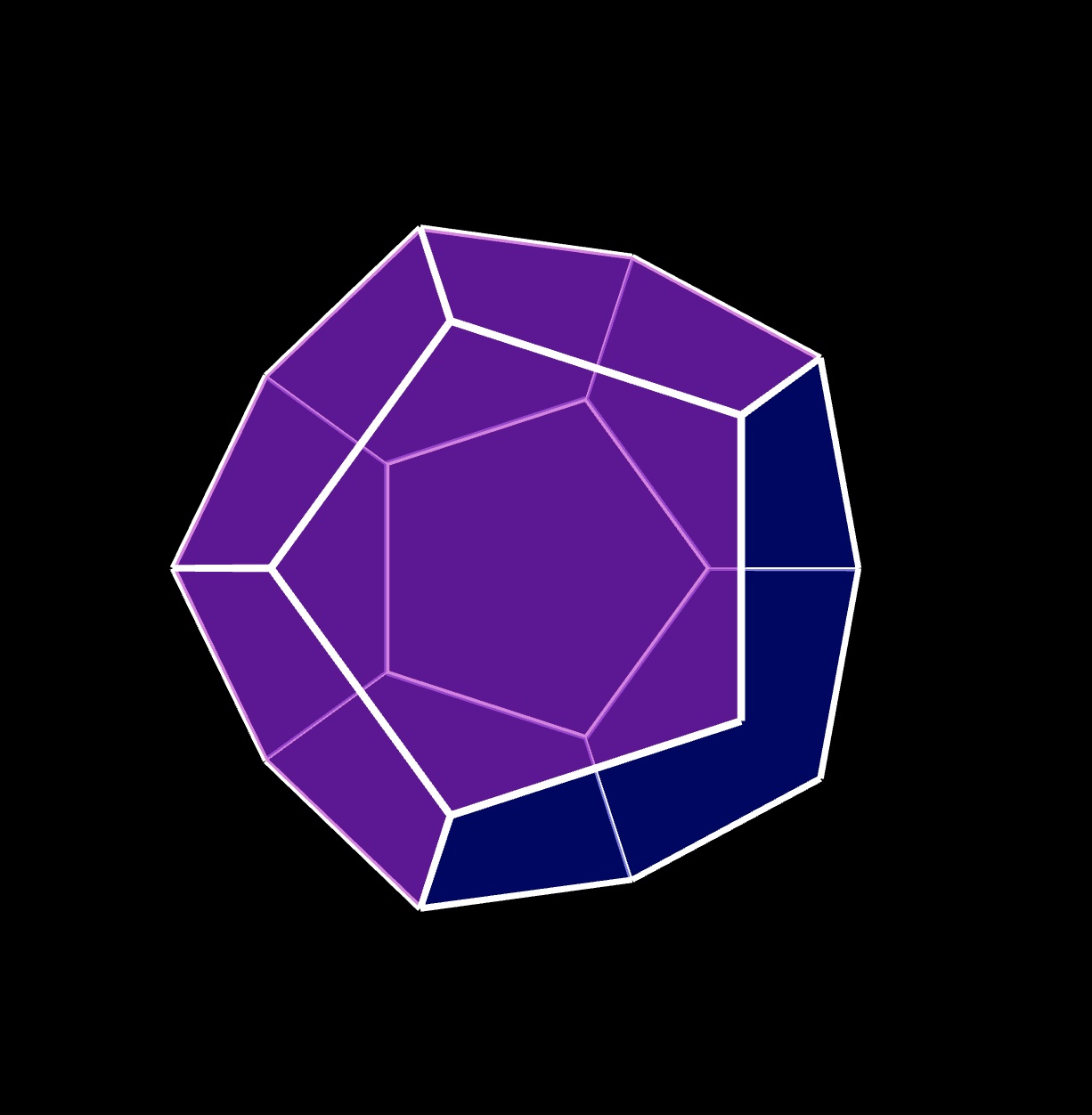
the 4th ⬠ adjacent to the top ⬠ :

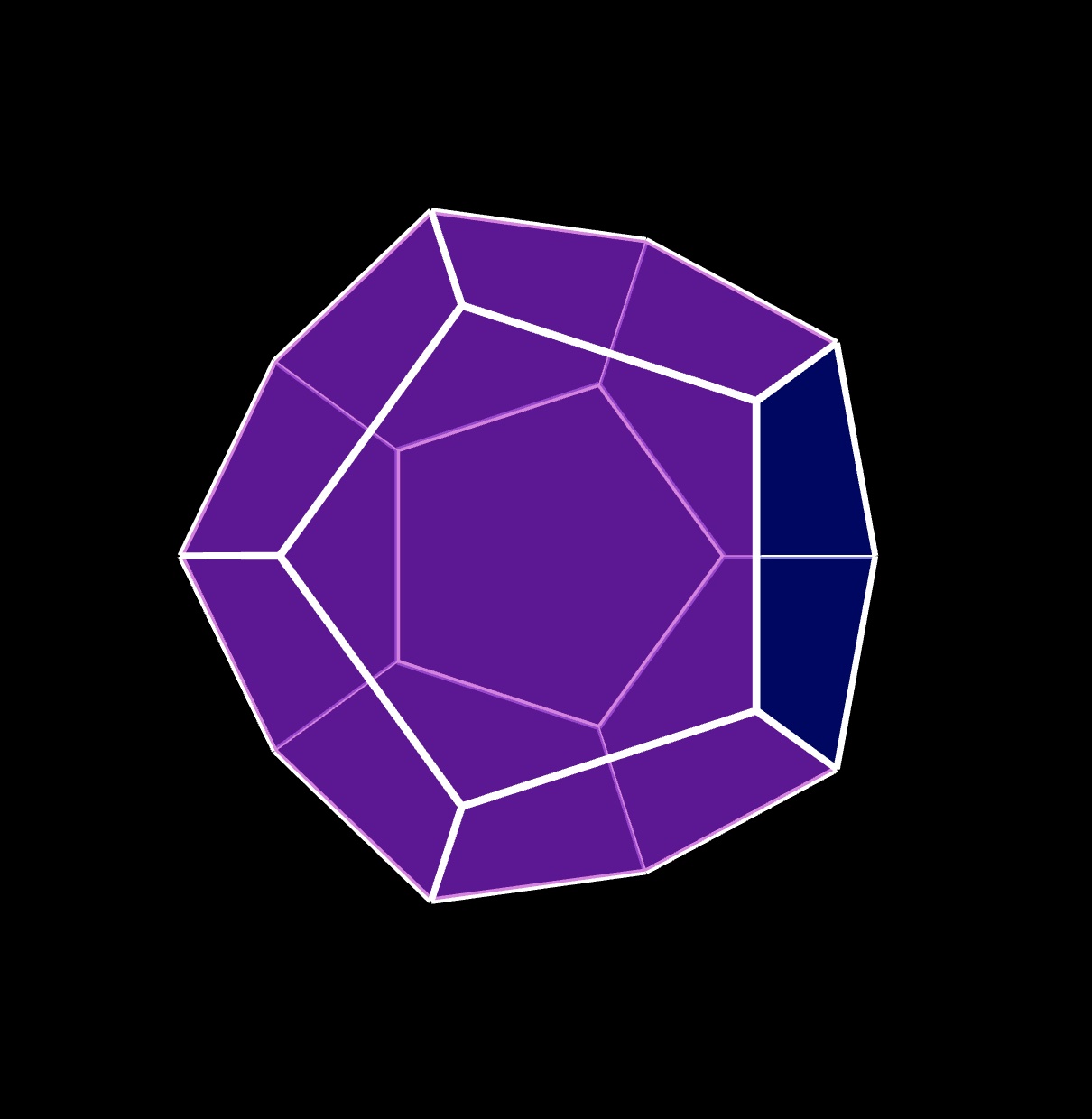
let ang = 0;
let r = 100;
let s,t,w,h;

function setup() {
  createCanvas(960, 960, WEBGL);
  stroke(255);
  strokeWeight(3);
  s = 2 * r * sin(PI/10);
  t = r * cos(TWO_PI/10);
  w = 2 * asin(sin(3*PI/10) / 
      sin(3*PI/5)); //116.7º
  let GE = 2*r*sin(PI/5)*sin(PI/5);
  let EH = r + t - GE;
  h = sin(w) * (2 * EH + GE);
}

function penta(){
  push();
  translate(t,0,0);
  beginShape();
  for(let a = 0; a < TWO_PI; 
    a += TWO_PI/5) {
    let x = r*cos(a);
    let y = r*sin(a);
    vertex(x, y);
  }
  endShape(CLOSE);
  pop();
}

function half(){
  push();
  translate(-t,0,0);
  penta();
  pop();

  push();
  for(let i=0;i<5;i++){
    rotateZ(TWO_PI/5);
    push();
    translate(-t,0,0);
    rotateY(-w);
    penta();
    pop();
  }
  pop();
}

function draw() {
  ang += 0.01;
  background(0);
  rotateY(ang);
  rotateX(ang*0.5);
  rotateZ(ang*0.2);

  push();
  fill(0,0,200,130);
  half();
  pop();

  push();
  fill(200,0,200,130);
  translate(0,0,h);
  rotateY(PI);
  half();
  pop();
}

    

ch 2.2 The Regular Polyhedra p22 of